Martingale is like this..If you go to roulette. You're looking to make 1 dollar.
You bet one on black, then you win! You accomplish your goal of making one dollar.
However. If you lose, you rebet 2 dollars on black, if you lose you bet 4 dollars.
You keep doubling your bet until you win. With inifnite money, you will never lose, the limit of your probility losing goes to 0.
The caveat lies in having infinite money, no one has infinite money so the probability is non zero.
But the mind wants to believe that that probabilty non zero is a lot smaller than what it actually is.
AS described from my coin flip experiment, it's actually more likely for that small chance to happen given a large amount of trials.

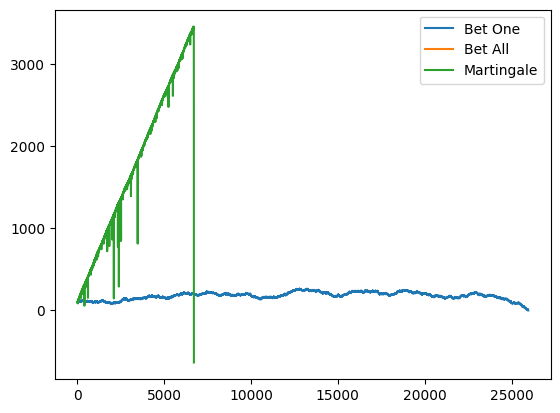
Based on my graph, yes you definitely lose. It's just the fact that it takes some time. Is there a statistical way to withdraw before that happens?
I'm not sure how easy that is to do. There has to be some math involving the complement. IE: quit before N losses so that your probability of winning is over P.
In other words. How many games must you play so that your probability of NOT LOSING is above 80% for example. I am a risk averse person (generally), so I would say that 80% is a good amount.
However, the risk is also relative to the amount gained. If I realize that that answer is 5 dollars for instance, I am willing to risk more to gain more.
This is more of a psychological problem because I need to calculate my own curve (non-linear thinking) of what percentage I'm willing to have NOT LOSING versus the amount of money I would like to gain
And then plot that against the martingale curve. And see where it intersects..
This is so confusing..